
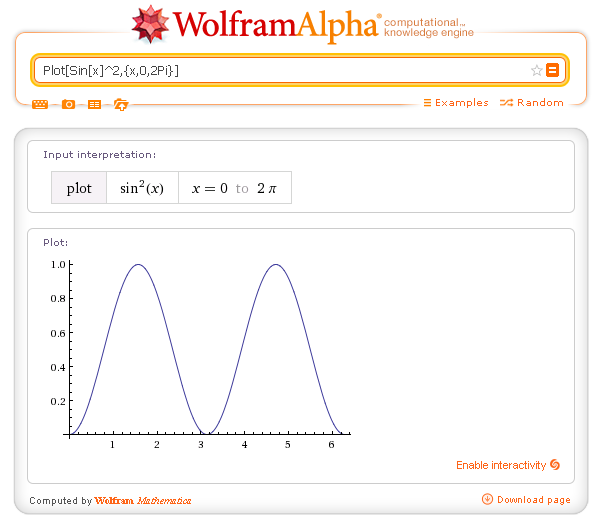
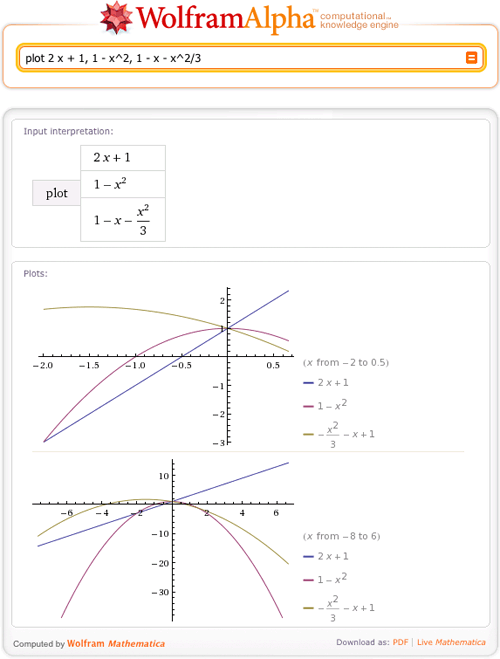
Here are a couple more examples to test out: Wolfram|Alpha will return an individual plot of each function in the list. What happens if you want to plot more than one bivariate function? In such cases you can always manually enter a plot range like we did in the example above.

#Wolframalpha grapher code
If Wolfram|Alpha fails to generate a plot, then it’s most likely because the code that determines a plot range has been unable toįind a region where the function has interesting behavior. Start by plotting y^2 cos( x) for x between -6 and 6 and y between -2 and 2.Īs in the univariate case, Wolfram|Alpha has the capability to find an appropriate plot range for a bivariate function, the code for which is under continuous development. Now let’s give Wolfram|Alpha a challenge and plot bivariate functions. The code can then be evaluated in Mathematica. By clicking the bottom left of the images and then “Copyable plaintext”, you can see the Mathematica code used to generate the plots. The underlying Mathematica function used in all the examples is Plot. You can also plot more than one function at a time. One important difference is that the image sizes are larger if you specifically ask for a plot. If we simply enter a univariate expression without the prefix “plot”, then we’ll always get a Cartesian plot in addition to a number of other pieces of information. So far we have told Wolfram|Alpha that we’re specifically requesting a plot. One of the unique features of Wolfram|Alpha is the functionality to automatically guess an appropriate plot range for univariate and bivariate functions. We still get back a plot with all of its defining features. What happens if we don’t give Wolfram|Alpha a range? In both these examples we have given Wolfram|Alpha a horizontal plot range. If we change √7 to √-7, then we get a plot of the real and imaginary parts. Here we plot sin(√7 x)+19cos( x) for x between -20 and 20. We will start simple with 2D Cartesian plots. Let’s take a look at the plotting functionality in Wolfram|Alpha, some of which is newly improved!
#Wolframalpha grapher series
Furthermore, in Wolfram|Alpha we can generate specialized plots for illustrating asymptotes, cusps, maxima, minima, inflection points, saddle points, solutions of ordinary differential equations, poles, eigenvalues, series expansions, definite integrals, 2D inequalities, interpolating polynomials, least-squares best fits, and more. Wolfram|Alpha is certainly not limited to Cartesian plotting we have the functionality to make number lines, 2D and 3D polar plots, 2D and 3D parametric plots, 2D and 3D contour plots, implicit plots, log plots, log-linear plots, matrix plots, surface of revolution plots, region plots, list plots, pie charts, histograms, and more. If you are feeling daring, enter a multivariate function, and the result will be a 3D Cartesian graph.
#Wolframalpha grapher full
Runs on powerful PC hardware: faster, more memory, full keyboards, screens, etc.Plotting functions in the Cartesian plane is such a simple task with Wolfram|Alpha: just enter the function you are looking to graph, and within seconds you will have a beautiful result.Support for peripherals such as gamepads, microphones, projectors, etc.Built-in slide show presentation mode ».Fully integrated document capabilities for student work, courseware, etc.Built-in access to extensive curated real-world datasets ».Immediate import of external data from files, devices and the web ».Efficient scalable computation allowing use of real-world examples.Full coverage of calculus, equation solving, etc.High-quality arbitrary-precision numerical computation ».Full support for note- and waveform-based sound ».State-of-the-art dynamic and animated graphics.Adaptive sampling in 2D and 3D plots for greater fidelity ».Thousands of classroom demonstrations immediately available ».Full easy-to-learn modern programming language ».Document-centered interface records calculation steps for review, reuse or sharing ».Easy-to-read typeset input and output ».Vastly more computational capabilities than any calculator ».Key Advantages of Mathematica Compared to Graphing Calculators: Finance, Statistics & Business Analysis.Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Data Framework Semantic framework for real-world data.


 0 kommentar(er)
0 kommentar(er)
